L’accroissement du trafic aérien national et international impose à chaque pays membre de l’OACI d’avoir une couverture en moyens de radionavigation aussi sûre et fiable que possible. Les balises V.O.R . en sont un des constituants importants.

Les balises V.O.R. conventionnelles remplissent parfaitement ce rôle lorsque leur site d’implantation ne présentent pas de difficultés particulières lorsque le site choisi est dégagé. L’installation d’une balise à proximité d’une zone montagnes devient plus problématique .

La qualité du signal étant tributaire des caractéristiques du site, le rayonnement directionnel de la balise ne peut être réfléchi par les obstacles se situant dans la zone de couverture de son émetteur, faute de quoi les réflexions diverses peuvent entacher le relèvement du QDM au point de rendre la mesure de ce dernier inutilisable.

Les erreurs en V.O.R. conventionnel
Principe du V.O.R. Doppler
Principe des émetteurs V.O.R. Doppler.
Le V.O.R. Doppler à bandes latérales alternées.

Les erreurs en V.O.R. conventionnel

Supposons un obstacle réfléchissant le rayonnement de la balise V.O.R. Le rayonnement émis emprunte deux trajets pour parvenir au récepteur V.O.R. situé à bord de l’aéronef.

Un premier trajet direct.
Un second trajet allant de la balise V.O.R. jusqu’à l’obstacle et une fois réfléchi par ce dernier vers l’aéronef.
Supposons que le deuxième trajet jusqu’à l’obstacle fasse une angle 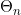$\Theta_n$ avec le trajet direct.
Supposons que le QDM réel soit égal à 0° (pour cet exemple).

On appelle $\beta$ le rapport d’amplitude entre le signal réfléchi (signal parasite) et celui du trajet direct (signal utile).

$\beta=\frac{V r\acute{e}fl\acute{e}chi}{V direct}$

$\Delta d$ = la différence de distance entre les deux chemins.

A la réception à bord de l’aéronef nous aurons deux signaux décalés de $\tau$ ce qui donne :

$V_1=V_0 \sin \omega t [1+K \cos \Omega_3 t + K \cos (\Omega_2 t + m \sin \Omega_3 t)]$

et ${\textstyle V_2=\beta V_0 \sin \omega (t-\tau)[1+K\cos(\Omega_3(t-\tau)-\Theta_2)+K \cos(\Omega_2(t-\tau)+m \sin \Omega_3(t-\tau))]}$

$\tau$ = temps pour parcourir $\Delta d$

$\tau = \frac{\Delta d}{c}$
avec c = vitesse de la lumière.

$c = \lambda . f \rightarrow \tau = \frac{\Delta d}{f}$

Dans $V_2 \omega \tau = 2 \pi \frac{f}{f} \frac{\Delta d}{\lambda}$ soit un angle de $\varphi = \frac{2\pi.\Delta d}{\lambda}$ représentant le retard de phase du signal parasite.

Erreurs sur la modulation à 30 Hz

Dans $\Omega_3 \tau = 2 \pi \frac{F_3}{f}.\frac{\Delta d}{\lambda}$ , or $F_3 = 30 Hz$ , $f \simeq 100 MHz$ soit $\lambda \simeq 3m$ , même si $\Delta d = 10 km$ le retard de phase sur la modulation est donc négligeable $\simeq$ 0,5 °. On peut donc le négliger par rapport à $\Theta_n$ , de l’ordre de plusieurs degrés.

Erreurs sur la modulation à 9960 Hz

$\Omega_2 \tau = 2\pi \frac{F_2}{f} . \frac{\Delta d}{\lambda}$

Avec $F_2 = 9960 Hz \rightarrow \Omega_2\tau \simeq$ 120°. Ce retard de phase est négligeable sur le fonctionnement du récepteur le résultat étant du même ordre que précédemment.
Ces effets sont donc négligeables, on peut exprimer le le signal parasite sous la forme :

$V_2= \beta \0 \sin(\omega t-\varphi) [1 + K \cos(\Omega_3 t - \Theta_n) + K \cos(\Omega_2 t + m \sin \Omega_3 t)]$

L’influence du signal parasite sur le signal utile on s’aperçoit que la modulation à 30 Hz est perturbée : le signal utile $y = \cos \Omega_3 t$ se trouve modulé en amplitude par $\sqrt{1 + 2 \beta \cos \Theta_2}$ et surtout déphasé de $\beta . \sin \Theta_n$

Donc une erreur d’information sur le QDM proportionnelle au rapport des amplitudes relatives $\beta$ et $\sin \Thetea_n$ ,
avec un rapport $\beta$ de 0,1 la courbe d’erreur est la suivante :

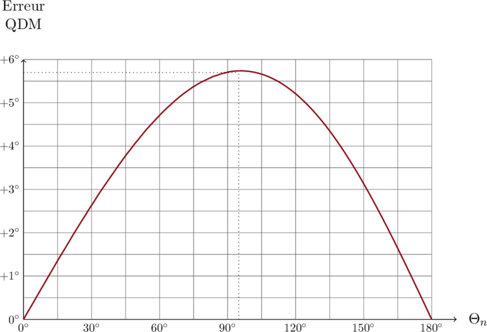
Le maximum d’erreur $\epsilon_{max}$ = 5,7° est atteint pour $\Theta_n$ = 95°

Pour éliminer cette cause d’erreur probable le système de génération des signaux a été changé.

Principe du V.O.R. Doppler

Afin de réduire les erreurs (probables) décrites au paragraphe précédent, les constructeurs ont eu l’idée d’inverser les modulations.

Le signal portant la Référence (porteuse modulée en AM à 30 Hz) est émis omnidirectionnellement. Ainsi, en cas de réflexion parasite, le signal réfléchi a la même phase que le signal direct, son effet est indépendant de son trajet.

Mais l’information phase variable doit donc moduler en fréquence la sous-porteuse 9960 Hz afin que l’émission reste compatible avec les récepteurs déjà en service.
Pour créer cette information on utilise l’effet Doppler créé par une antenne tournante.

Principe

Soit une antenne mobile, décrivant un cercle de rayon $R$ , avec une vitesse angulaire $\Omega_3$

A l’instant $t$ l’antenne fait un angle $\alpha = \Omega_3 t$ avec le nord magnétique.
Le signal reçu par un récepteur dans la direction $\Theta$ sera donc décalé dans le temps par rapport à la réception du signal émis par une antenne omnidirectionnelle placée au centre du cercle O.

Ce temps $\tau$ correspond à :

$\tau = \frac{l}{c}$

$l$ représente la longueurs OH, soit $l = R \cos(\alpha - \Theta)$

Le signal provenant de A sera donc déphasé par rapport au signal émis par l’antenne O.

Réception provenant de O : $V_1 = V_0 \cos(\omega t)$
Réception provenant de A : $V_2 = V_0 \cos(\omega t - \varphi)$

avec $\varphi = \frac{2\pi.R}{\lambda} \cos(\alpha - \Theta)$

Le signal $V_2$ sera $V_2 = V_0 \cos [\omega t - \frac{2\pi.R}{\lambda} \cos(\Omega_3 t - \Theta)]$ , c’est à dire un signal modulé en phase, d’indice $m$ :

$m = \frac{2\pi.R}{\lambda}$

par un signal BF $\cos \Omega_3 t$
avec une phase $\Theta$

En disposant 3 antennes on reconstitue le signal V.O.R.

une antenne fixe au centre O, émettant un signal $V_1 = V_0 \cos 2\pi.f.t(1 + K \cos \Omega_3 t)$
une antenne mobile au point A décrivant le cercle de rayon R, alimentée par une fréquence décalées de F2 = + 9960 Hz par rapport à la porteuse; soit : $V_2 = V_0 \cos [2\pi(F + F2)t + \frac{2\pi.R}{\lambda}.\cos(\Omega_3 t - \Theta)]$ (lorsque l’antenne tourne à 30 t/s).
Une autre mobile, située en A’,diamétralement opposée au point A et décalée de – 9960 Hz en fréquence, elle tourne à la même vitesse angulaire, soit : $V_3 = V_0 \cos [2\pi(F - F2)t + \frac{2\pi.R}{\lambda}.\cos(\Omega_3 t - \Theta)]$

A la réception la somme des deux signaux donne :

C’est l’équivalent d’un signal V.O.R. conventionnel à ceci prés que l’information d’azimuts est contenue dans la modulation de fréquence.

$V_R = V_0 \cos \omega t[1 + K \cos \Omega_3 t + K \cos(\Omega_2 t + m \cos(\Omega_3 t - \Theta))]$

Pour assurer la compatibilité avec les récepteurs V.O.R. conventionnels, la rotation des antennes doit s’effectuer en sens inverse (du V.O.R. conventionnel). Ainsi il n’est pas nécessaire de remplacer toute une flotte de récepteurs V.O.R.

Dans la figure ci-dessus, le rayon R et la fréquence de travail déterminent l’indice de modulation m, lequel est imposé à 16.
Ce qui implique que : $R.\Omega_3 = \frac{m.\lambda}{2\pi}.2 \pi.F_3$ -> 1250 m/s avec $F_3$ = 30 Hz et $\lambda$ = 2,6 m (à 115 MHz).

Le cercle doit avoir un rayon de $R = \frac{m.\lambda}{2\pi}$ soit 6,65 mètres.

Réalisation d’aérien tournant

Pour ne pas avoir à faire tourner un réseau d’antennes de plus de 6 mètres de diamètre à 30 t/s, on les remplace par une série d’antennes fixes équiréparties sur le cercle et alimentées à tour de rôle.

Il faut faire un échantillonnage du signal de manière à ce que la déformation reste acceptable lors des sauts d’antennes. La condition est $< \frac{2\pi}{3}$ ce qui implique au moins 3 échantillons sur une longueur d’onde.

La circonférence du cercle est imposée par l’indice de modulation m = 16.

$m = \frac{2\pi}{\lambda} \rightarrow 2.\pi.R = m.\lambda$

Pour N antennes espacées de $\frac{\lambda}{3}$ sur la circonférence on doit avoir $N.\frac{\lambda}{3}= m.\lambda \rightarrow N=3 & m$ .

Pour m = 16, N = 48 antennes.

*Construction des antennes V.O.R. Doppler*

Si l’on commute instantanément les antennes (signaux carrés) le spectre engendré est très large et perturbe les canaux voisins.
Pour diminuer la largeur de spectre, on effectue une commutation progressive des antennes à l’aide de demi sinusoïdes.

En fonction de $\alpha = \Omega_3 t$ les aptitudes des signaux en BLI et BLS varient donc progressivement et les phases de ces signaux varient par saut à chaque changement d’antenne.

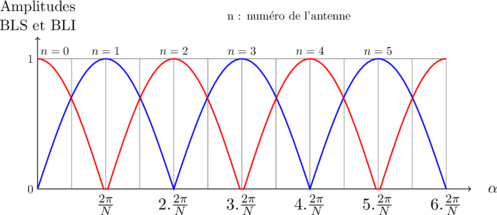
On alimente simultanément une antenne par la BLS et l’antenne diamétralement opposée par la BLI.

Il faut donc un nombre pair d’antennes.

Synoptique d’un émetteur V.O.R. Doppler

*Synoptique de principe d’un émetteur D-VOR*

Les fonctions $F(t)$ et $F(t+\gamma )$ sont deux fonctions permettant de faire varier les amplitudes de manière progressive.
On a donc, à un instant donné, 4 antennes en service (en plus de l’antenne de référence). Un jeu de commutateurs statiques permet de les alimenter.

Réseau d’antennes D-VOR

Chaque antenne est constituée d’une boule rayonnante dans le plan horizontal.
Les 48 antennes sont montées sur un contrepoids de 27 m de diamètre, situé à 3 m du sol.
Chaque antenne se trouve sur un cercle de 13,5 m de diamètre et à 1,3 m au dessus de la surface du contrepoids.

Ainsi est réalisée l’antenne dite « variable ».

Une antenne centrale rayonne le signal de référence.

Modulations parasites du V.O.R. Doppler

La contrepartie du système du système de commutation des antennes est l’apparition de modulation parasites. Le signal V.OR. est de la forme :

$S=A \sin(\Omega_3-\psi)$ (pour le 9960 Hz)

Ce signal est modulé à la fois en amplitude et en phase.

Modulation d’amplitude parasite

Cette modulation d’amplitude parasite se décompose en 2 modulations :

${A^2} = 1 + \sin \frac{\pi}{T_0}(t - nT_0).\cos [m\alpha . \sin(\Theta - (n + \frac{1}{2})\alpha)]$

Une enveloppe de modulation en 1/2 sinusoïdes à la fréquence de commutation des antennes, soit 48 x 30 = 1440 Hz.
Une deuxième enveloppe à la fréquence double de la rotation soit 60 Hz.

L’amplitude de ces modulations parasites est de l’ordre de 30%, mais les récepteurs V.O.R. y sont peu sensibles car ils assurent un pré-traitement du signal par ecrêtage avant démodulation.

Modulation de phase parasite

La phase du 9960 Hz est porteuse de l’information d’azimut.

$\tan \psi = \frac{A_n \sin \varphi_n + A_{n+1} \sin \varphi_{n+1}}{A_n \cos \varphi_n + A_{n+1} \cos \varphi_{n+1}}$

Comparée à la modulation théorique $\psi_{theo} = m \cos(\Theta - \Omega_3 t)$ la différence de phase a une valeur crête de 5,5°.
Comparé au signal de modulation qui a une valeur crête de 16 radians $\simeq$ 917°, le signal d’erreur ne représente que 0,6 % du signal principal.

Les premiers essais de V.O.R.-D eurent lieu en 1958 à Indianapolis sous l’égide de la CAA et confirmèrent la théorie. Leur implantation dans des régions où les V.O.R. conventionnels étaient inexploitables, notamment les régions montagneuses, permirent aux services de la navigation d’autoriser le pilotage automatique lors de leur survol, ce qui était jusqu’alors impossible.

Erreurs de relèvement en V.O.R.-D

L’erreur de QDM introduite est considérablement diminuée :

$\epsilon = \frac{\beta}{m} \cos \varphi [2J_1(2 m \sin \frac{\Theta_n}{2}) . \cos \frac{\Theta_n}{2}]$

Dans le cas du V.O.R. conventionnel l’erreur maximale atteint : $\varepsilon_{max}$ = 5,7° pour $\Theta_n \simeq$ 95°

Dans le cas du V.O.R.-D elle est de $\varepsilon_{max}$ = 0,4° pour $\Theta_n \simeq$ 7°, soit un rapport voisin de 16.

Principe des V.O.R. Doppler à bandes latérales alternées

La contrepartie du V.O.R. Doppler est son encombrement au sol, sa complexité d’installation et de mise au point. C’est pourquoi certains industriels ont envisagé de diminuer le nombre d’antennes afin de réduire le coût, tout en gardant les avantages du principe.

Partant du principe que l’information V.O.R. est redondante, car portée par les 2 bandes latérales, l’idée est d’en émettre qu’une.

Pour éviter que la qualité du signal soit altérée par :

une modulation parasite d’amplitude à 30 Hz ayant une phase variable avec l’azimuth.
Une modulation de phase provoquée par l’émission d’une bande latérale unique, perturbatrice lorsqu’il existe un écart de phase entre la réception des bandes latérales et la porteuse.

Pour différencier les deux types de V.O.R. on utilise les sigles suivants :

V.O.R. Doppler double bandes latérales : D-VOR DSB.
V.O.R. Doppler à bandes latérales alternées : D-VOR ASB.

Le principe est donc d’émettre alternativement la bande latérale supérieure puis la bande latérale inférieure.

On dispose sur un cercle un nombre N impair d’antennes équiréparties.

On alimente l’antenne $n$ par la bande latérale supérieure : $A_n \sin (\omega + \omega_2) t$

Et l’antenne $n + \frac{N - 1}{2}$ , puis l’antenne $n + \frac{N + 1}{2}$ par la bande latérale inférieure, soit $A \gamma \sin(\omega - \Omega_2) t$

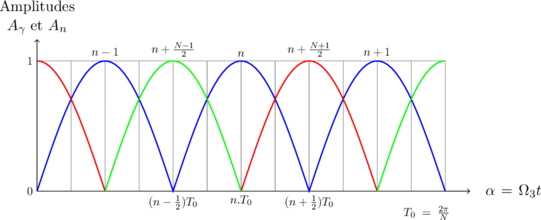
La somme des bandes latérales sera donc $S = A_n \sin((\omega + \Omega_2) t - \varphi_n) + A_\upsilon \sin((\omega - \Omega°2) t - \varphi_\upsilon)$ , ce qui peut s’écrire :

$S = \sin \omega t [A_n \cos(\Omega_2 t - \varphi_n) + A_\upsilon \cos(\Omega_2 t + \varphi \upsilon)] + \cos \omega t [A_n \sin (\Omega_2 t - \varphi_n) + A_\upsilon \sin (\Omega_2 t + \varphi_\upsilon)]$

Ce principe présente des caractéristiques de modulations parasites plus importantes que pour le D-VOR DSB.

Conclusion

Chaque système apporte ses avantages et ses inconvénients.

Le VOR conventionnel
- conception simple
- encombrement minimum
- coût modéré
- tributaire des situations géographiques en ce qui concerne les réflexions parasites.
Le D-VOR
- Meilleure tenue aux réflexions parasites
- Aériens plus encombrants
- coût plus élevé que pour le VOR conventionnel
- susceptibilité aux déphasages HF plus grande avec le D-VOR ASB que pour le D-VOR DSB.
- simplicité (relative) de mise en oeuvre pour le D-VOR ASB
- coût d’installation supérieur en D-VOR DSB par rapport au D-VOR ASB.

Références :

Simulateur de balises VOR conventionnel Doppler DSB et ASB / Mémoire d’ingénieur CNAM – Daniel MARTEAU – 1982.

Le V.O.R. Doppler